TimeStored Blog

Finding Pi using Monte Carlo Simulations in kdb q

In a previous post I looked at using the monte carlo method in kdb to find the outcome of rolling two dice. I also posed the question:

How can we find the value of Pi using the Monte Carlo method?

If we randomly chose an (x,y) location, we could calculate the distance of that points location ( sqrt[x²+y²] ) from the origin, this would tell us if that point lay within a circle or outside a circle, by whether the length was greater than our radius. The ratio of the points that fall within the circle relative to the square that bounds our circle, gives us the ratio of the areas.

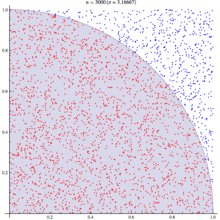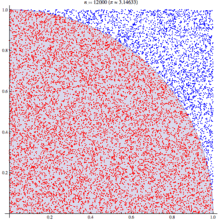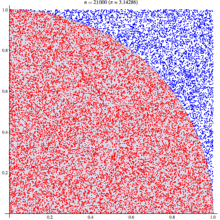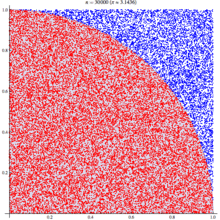
A diagram is probably the easiest way to visualize this problem. If we generate two lists of random numbers between -1 to 1. And use those as the coordinates (x,y), then create a scatter plot that plots (x,y) in one colour where x²+y² is greater than 1 and a different colour where it is less than 1, we would find a pattern emerging…in qStudio it looks like this:

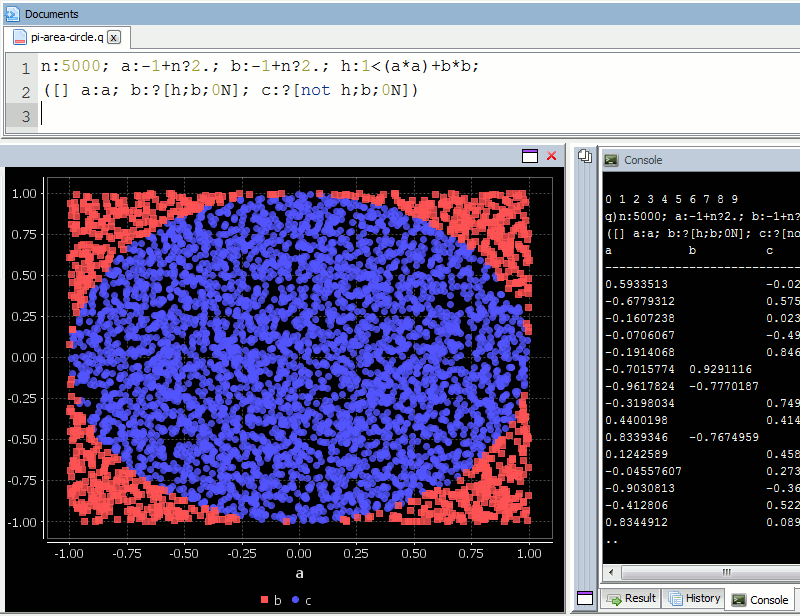
We know the area of our bounding square is 2*2 and that areaOfCircle=Pi*r*r, where r is 1. Therefore we can see that:


areaOfCircle = shadedRatio*areaOfSquare
Pi = shadedRatio * 4

q)4*sum[not h]%count h
3.141208


The wikipedia article on monte carlo method steps through this same example, as you can see their diagram looks similar:

Solving the Birthday Paradox in kdb q

In a previous post I looked at using the monte carlo method in kdb to find the outcome of rolling two dice. I also posed the question:

How many people do you need before the odds are good (greater than 50%) that at least two of them share a birthday?

In our kdb+ training courses I always advise breaking the problem down step by step, in this case:

1. Consider making a function to examine the case where there are N people.
2. Generate lists of N random numbers between 0-365 representing their birthdays.
3. Find lists that contain collisions.
4. Find the number of collisions per possibilities examined.
5. Apply our function for finding the probability for N people to a list for many possibilities of N.

In kdb/q:

Plotting our data in using qStudio charting for kdb we get:

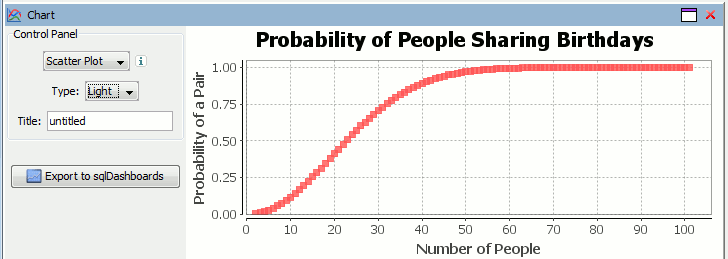
Therefore as you can see from either the q code or the graph, you need 23 people to ensure there’s a 50% chance that atleast 2 people in the room share a birthday. For more details see the wikipedia page. This still leaves us with the other problem of finding Pi using the monte carlo method in kdb.

Probability of a 12 when you roll two Dice

Performing probability questions in kdb/q is simple. I recently got asked how to find the probability of rolling a sum of 12 with two dice. We’ll look at two approaches to finding the likely outcomes in kdb/q:

Method 1 – Enumeration of all possibilities

Step by step we:

1. Generate the possible outcomes for one die.
2. Generate all permutations for possible outcomes of two dice, find the sum of the dice.
3. Count the number of times each sum occurs and divide by all possible outcomes to get each probability.

Method 2 – Monte Carlo Simulation

Alternatively , if it hadn’t occurred to us to use cross to generate all possible outcomes, or for situations where there may be too many to consider. We can use Monte Carlo method to simulate random outcomes and then similarly group and count their probability.


q)1+900000?/:6 6 / random pairs of dice rolls
2 5 6 6 2 4 3 1 5 1 1 4 6 5 3 4 2 4 1 2 3 6 6 1 1 3 6 3 6 2 3 1 5 4 4 4 6 3 1 3 1 2 5..
4 4 4 5 1 4 3 6 5 1 4 4 3 4 1 1 1 5 4 5 2 4 4 4 5 2 1 2 6 5 2 4 3 1 4 2 1 1 3 4 6 5 1..
q)/ same as before, count frequency of each result
q)(2+til 11)#{x%sum x} count each group sum each flip 1+900000?/:6 6
2 | 0.02766
3 | 0.05559
4 | 0.08347
5 | 0.11085
6 | 0.1391822
7 | 0.1669078
8 | 0.1386156
9 | 0.1112589
10| 0.08317222
11| 0.05556222
12| 0.02773111


Therefore the probability of rolling a sum of 12 with two dice is 1/36 or 0.27777. Here’s the similar dice permutation problem performed in java.

Kdb Problem Questions

If you want to try using the monte carlo method yourself try answering these questions:

1. The Birthday Paradox: How many people do you need before the odds are good (greater than 50%) that at least two of them share a birthday?
2. Finding the value of Pi. Consider a square at the origin of a coordinate system with a side of length 1. Now consider a quarter circle inside of the square, this circle has a radius of 1, therefore its area is pi/4. For a point (X,Y) to be inside of a circle of radius 1, its distance from the origin (X ², Y²) will be less than or equal to 1. We can generate random (X,Y) positions and determine whether each of them are inside of the circle. The ratio of those inside to outside will give the area. (bonus points for using multiple threads)