Solving the Birthday Paradox in kdb q »

Solving the Birthday Paradox in kdb q

December 10th, 2013 by Ryan Hamilton

In a previous post I looked at using the monte carlo method in kdb to find the outcome of rolling two dice. I also posed the question:

How many people do you need before the odds are good (greater than 50%) that at least two of them share a birthday?

In our kdb+ training courses I always advise breaking the problem down step by step, in this case:

Consider making a function to examine the case where there are N people.
Generate lists of N random numbers between 0-365 representing their birthdays.
Find lists that contain collisions.
Find the number of collisions per possibilities examined.
Apply our function for finding the probability for N people to a list for many possibilities of N.

In kdb/q:

q){x cut (x*99909)?365} 4 / consider it for 4 people
340 217 139 191
12  295 15  113
344 206 161 203
351 45  181 344
138 47  311 205
41  224 271 223
283 47  77  77
..

q)/ sort each list of numbers and then check for numbers the same beside each other
q)/ here we use the adverbs ': each previous and ' each
q)(=':') asc each {x cut (x*99909)?365} 4
0000b
0000b
0000b
0000b
0000b
0000b
0010b
..
q)/ where any collisions occur return true
q)any each (=':') asc each {x cut (x*99909)?365} 4
0000000000000000000000000000000000000000000000000000000000000000000000000001000000000..

q)/ find the probability
q){(sum x)%count x} any each (=':') asc each {x cut (x*99909)?365} 4
0.01580438

q)findProb:{{(sum x)%count x} any each (=':') asc each {x cut (x*99909)?365} x}
q)/ find the probality for N people from 2 to 101
q)t:update prob:findProb peach a from ([] a:2+til 100)
q)t
a  prob
--------------
2  0.002752505
3  0.008357605
4  0.01603459
5  0.02655416
6  0.04084717
7  0.05693181
8  0.07378715
9  0.09346505
10 0.1160856
..
q)exec first a from t where prob>0.5
23

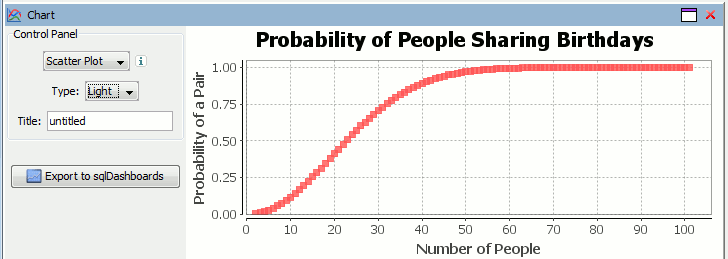
Plotting our data in using qStudio charting for kdb we get:

Therefore as you can see from either the q code or the graph, you need 23 people to ensure there’s a 50% chance that atleast 2 people in the room share a birthday. For more details see the wikipedia page. This still leaves us with the other problem of finding Pi using the monte carlo method in kdb.

No Comments

TimeStored Blog

Solving the Birthday Paradox in kdb q